モンテカルロ法で円周率の近似値を求める

「エクセル 円周率 求め方モンテカルロ法」
「乱数を利用した円周率の求め方 excel」
といった検索キーワードで、このサイト『インストラクターのネタ帳』へのアクセスがありました。

モンテカルロシミュレーションを行って、円周率の近似値をExcelで計算するには、どうすればいいのかを探していた方による検索です。

モンテカルロ法で円周率の近似値を求めるワークシート

下図のような形で、A:B列に乱数を発生させ、円の面積の近似値をJ列で計算するワークシートを作る例を、この記事ではご紹介します。

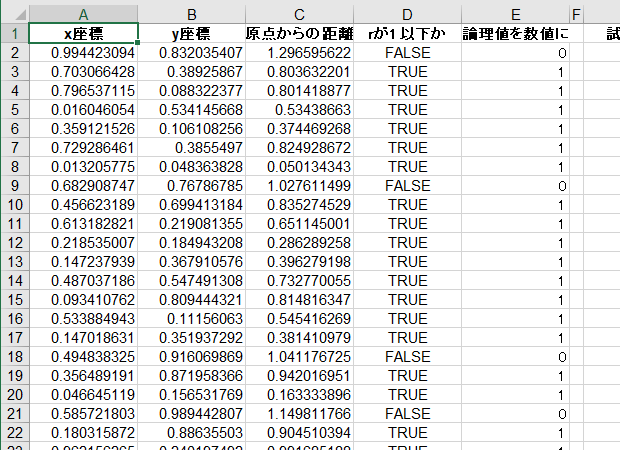
A列にx座標の乱数、B列にy座標の乱数を、C列にx座標とy座標から計算した原点からの距離（すなわち円の半径r）、D列に半径rが1以下か否かの論理値、E列にD列の論理値を数値にした1または0を出力します。

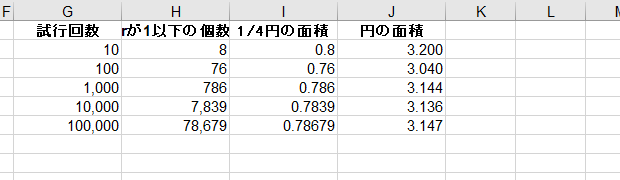
G列には何回試行したか、H列に半径rが1以下のデータの個数、I列に1/4円の面積の近似値、J列に半径1の円の面積（すなわち円周率）の近似値を出力します。

x座標・y座標と半径rが1以下かを出力する部分の作成

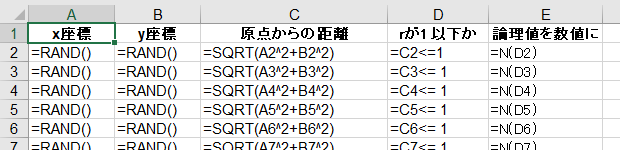
ランダムに打った点のx座標・y座標と、半径rが1以下かを出力するA:E列には、以下のような数式を入力します。

モンテカルロ法を使った円周率の近似値計算を熟知している方なら、C2:E2セルをまとめてイイと思いますが、初めての方は、上述のように計算式をバラバラにしておくほうが理解しやすいはずです。

C列にはピタゴラスの定理を真面目に入力していますが、原点からの距離が1以下かどうかが判定できればイイだけですから、SQRT関数を削除した
　　=A2^2+B2^2
でもOKです。

E列の数式ではN関数を使って論理値を数値にしていますが、
　　=D2*1
でもOKです。

円の面積の近似値を推測する部分の作成

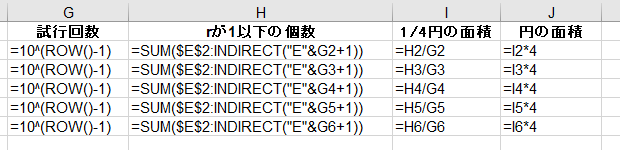
上述のE列の値を使って、半径rの円の面積の近似値を推測するG:J列は以下のとおりです。

H2セルの数式、
　　=SUM($E$2:INDIRECT("E"&G2+1))
は、この後オートフィルするためにちょっと難しくなっています。
この数式は、モンテカルロ法で円周率の近似値を計算する本筋とは関係なく、オートフィルで複製できるようにINDIRECT関数を使っているだけですから、合計を計算する数式を個別に入れてもイイでしょう。

INDIRECT関数を使わない場合、
H2セルに
　　=SUM(E2:E11)
H3セルに
　　=SUM(E2:E101)
H4セルに
　　=SUM(E2:E1001)
H5セルに
　　=SUM(E2:E10001)
H6セルに
　　=SUM(E2:E100001)
をそれぞれ入力してください。これらの数式のほうが、何を合計しているのかがわかりやすいはずです。

I列には、試行回数のうち半径rが1以下の数がどれくらいの比率なのかを計算することで、半径rが1の1/4の面積の近似値を計算しています。この値を4倍すれば円の面積になります。

円周率と円の面積の関係

そもそも円周率とは、直径に対する円周の比率です。これに対して上述のモンテカルロ法で求めているのは、あくまでも円の面積の近似値です。

なぜこの円の面積が円周率に近似するかがピンと来ない方は、円の面積の公式を思い出してください。

円の面積は「π×半径の2乗」で計算できます。ということは、半径が1であれば、面積はπと同じになるわけです。

実教出版『最新 情報の科学』情科307について思うこと

高校の授業『情報の科学』では、モンテカルロ法に触れる場合もあるようです。

2020年現在採用されている『情報の科学』の文部科学省検定教科書のうち、実教出版の『最新 情報の科学 新訂版』情科307の、「3章 問題解決のためのコンピュータ活用 3節 モデル化とシミュレーション」には、モンテカルロ法を使って円周率を求める方法が掲載されています。

この『最新 情報の科学 新訂版』について、折角モンテカルロ方を扱うのなら、改善して欲しいと感じる部分があります。

モンテカルロシミュレーションの試行回数

実教出版の『最新 情報の科学 新訂版』のp.101では、試行回数を「100」から「1000」まで100ずつ増やしているのですが、これでは試行回数を増やすに従ってπに近似していく様子を観察できないはずです。上述のように試行回数はべき乗で増やしていかないと、意味がないだろうと感じます。

論理式・論理値を使って欲しい

円の内部にある点の個数をカウントするのに、『最新 情報の科学 新訂版』ではCOUNTIF関数を使っているのですが、折角『情報の科学』という科目なのですから、ここは論理式や論理値を明確にした例にしてもイイんじゃないかなぁと思っています。

最終更新日時：2020-11-15 08:07